OBJETIVO(S) GENERAL(ES)
DE LA ASIGNATURA:
Al término del curso el
alumno reconocerá los esfuerzos y deformaciones de sólidos sujetos a estados
generales de cargas, que le permitirán solucionar problemas de mecánica de
materiales en la ingeniería mecatrónica.
TEMAS Y SUBTEMAS
1. FUERZA AXIAL,
CORTANTE Y MOMENTO FLEXIONANTE
1.1. Diagramas de fuerza
cortante
1.2. Diagramas de
momento flexionante
1.3. Método por
secciones
1.4. Método por
integración
2. EL ANÁLISIS DE
ESFUERZO
2.1. Esfuerzo normal
debido a una carga axial
2.2. Esfuerzo cortante
2.3. Esfuerzo de apoyo
2.4. Factor de seguridad
3. EL ANÁLISIS DE
DEFORMACIÓN
3.1. Concepto de
deformación
3.2. Deformación axial
3.3. Deformación
multiaxial
3.4. Deformación térmica
4. ELEMENTOS SUJETOS A
TORSIÓN
4.1. Torsión en vigas de
sección circular
4.2. El cálculo de
árboles de transmisión de potencia
4.3. Ángulo de torsión
4.4. Torsión de barras
circulares
5. ESFUERZOS POR FLEXIÓN
EN VIGAS
5.1. Flexión en vigas
5.2. Ángulo de flexión
5.3. Efectos combinados
5.4. Flexión en vigas
curvas
6. ESFUERZOS COMBINADOS
6.1. Círculo de Mohr
para esfuerzos
6.2. Análisis de
esfuerzo bajo cargas combinadas
6.3. Estructuras
6.4. Columnas
6.4. Columnas
Mecánica de materiales
Concepto: Es una rama de la mecánica que estudio los efectos internos del esfuerzo y la deformación en un cuerpo solido que esta sometido a una carga externa. El esfuerzo se encuentra asociado con la resistencia del material del que está echo el cuerpo.
Equilibrio de un cuerpo deformable
La estatica es el análisis de cuerpos en equilibrio, incluidos los operadores robóticos, los puentes, las presas y los edificios.
En este capítulo se estableceran las ecuaciones de qiuilibrio y discribimos modelos sencillos de los diversos tipos de soportes utilizados en ingeniería.
La estatica es el análisis de cuerpos en equilibrio, incluidos los operadores robóticos, los puentes, las presas y los edificios.
En este capítulo se estableceran las ecuaciones de qiuilibrio y discribimos modelos sencillos de los diversos tipos de soportes utilizados en ingeniería.
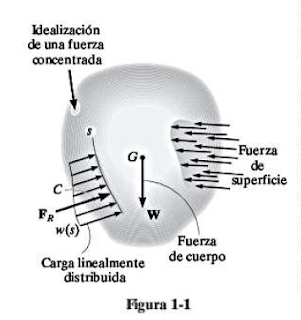
Cargas externas.
Un cuerpo que esta sometido a dos tipos de cargas externas, es decir las fuerzas de superficie o las fuerzas de cuerpo. Como se meustra en la siguente imagen 1.1
Fuerzas de superficie: Son causadas por el contacto directo de un cuerpo con la superficie de otro, las fuerzas de superficie pueden liderarse como una solo fuerza concentrada que se aplica a un punto sobre el cuerpo, algunos ejemplos podrían ser la ruda de la bicicleta, hasta de al bandera, el sube y baja.
Fuerzas de campo: Se desarrolla cuando un cuerpo ejerce una fuerza sobre otro cuerpo sin contacto físico directo entre esto. El ejemplo claro seria la gravedad y electromagnético.
Reacciones en los soportes (apoyos).
Las fuerzas de superficie que se desarrollan en los soportes o puntos de contacto entres los cuerpos se llama reacción. En la siguiente tabla se muestra los soportes más comunes para los problemas bidimensionales, es decir, para cuerpos sometidos a sistemas de fuerza coplanares. Observe con cuidado el simbolo utilizado para representar cada soporte y el tipo de reacciónes que ejerce sobre el elemento con el que está en contacto. Como regla si el soporte impide la traslación en una dirección dada, entonces debe desarrollarse un fuerza sobre el elemento en esa dirección. Del mismo modo, debe ejercerse un momento sobre el elemento. Por ejemplo, un soporte de rrodillo solo puede impedir la traslacion perpendicular o normal a la superficie.
Ecuaciones de equilibrio.
El equilibrio de un curpo requiere un balance de furzas para impedir que el cuerpo se traslade o tenga un movimiento acelerado a lo largo de una trayectoria recta o curva, y un balance de momento para impedir que el cuerpo gire. Estas condiciones pueden expresarse de manera matematica mediante dos ecuaciones vectoriales.
UNIDAD 2: ESFUERZO

Deformación (δ) se refiere a los cambios en las dimensiones de un miembro estructural cuando este se encuentra sometido a cargas externas.
Estas deformaciones serán analizadas en elementos estructurales cargados axialmente, por los que entre las cargas estudiadas estarán las de tensión o compresión.
Un ejemplo de ellos:
DEFORMACIÓN UNITARIA
El equilibrio de un curpo requiere un balance de furzas para impedir que el cuerpo se traslade o tenga un movimiento acelerado a lo largo de una trayectoria recta o curva, y un balance de momento para impedir que el cuerpo gire. Estas condiciones pueden expresarse de manera matematica mediante dos ecuaciones vectoriales.
Si se fija un sisitema de coordenadas x,y,z con el origen en el puento 0, los vectores de fuerza y de momento pueden separerse en componentes a lo largo de los ejes coordenados y en las dos ecueciones anteriores pueden escribirse en forma escalar como seis ecueciones, consideradas como.
Con frecuencia, en la practica de la ingenieria, la carga sobre un cuerpo puede representarse como un sistema de fuerza se encuentran en el plano x-y, entonces las condiciones para el equilibrio del cuerpo pueden especificarse mediante solo tres ecuaciones escalares de equilibrio, que son:
Cargas internas resultantes.
En la mecanica de materiales, la estática se usa principalmente para determinar las cargas resultante que actúan dentro de un cuerpo. Por ejemplo asi como se muestra en la figura (a) de abajo que se mantiene en equilibrio mediante las cuatro fuerzas externas. A fin de obtener las cargas internas que actúan sobre un region específica dentro del cuerpo, es necesario hacer una sección imaginaria o "corte" através de la región donde van determinarse las cargas internas. Despues las ods partes del cuerpi se separan y se dibuja un diagrama de curpo libre de una de las partes, figura (b). Aunque la distribución exacta de la carga interna puede ser desconocida, pueden usarse las ecuaciones de equilibrio para relacionar las fuerzas eternas sobre la parte inferior del cuerpo conla fuerza y el momento de resultante de la distrabucion, en cualquier puento especifico o sobre el area secciónada, figura (c).
Tres dimenciones: Con la distribucion de fuerza en el área seccionada y se desarrollarán ecuaciones que puedan usarse para el análisis y diseño del cuerpo. Entonces, puede definirse cuatro diferentes tipos de carga resultantees de la siguente manera:
Fuerza normal, N. Esta fuerza actúa perpendicularmente al área. Se desarrolla siempre que las cargas externas tienden a empujar o jalar sobre los dos segmentos del cuerpo.
Esfuerzo cortante, V. Se encuentra en el plano del área y se desarrolla cuando las cargas exteras tienden a ocasionar que los dos segmentos del cuerpo se deslicen uno sobre el otro.
Momento de torsión o torque, T. Este efecto se desarrollacuandolas cargas externas tienden a torcer un semento del cuerpo con respecto al otro alrededor de un eje perpendicular al área.
Momento flexionante, M. Es causado por las cargas externas que tienden a flexionar el cuerpo respecto a un eje que se encuentra dentro del plano del área.
Cargas coplanares.
Si el cuepo está sometido a un sistema de fuerzas coplanares, figura (a), entonces en la seción sólo existen componentes de fuerzas mormal, de fuerza cortante y de momento flexionante, figura (b).
Aplicaciones bidimensionales
Soportes
Estado de pie, el piso nos soporta; sentados en una silla, ésta nos soporta.
Ahora veremos cómo los cuerpos se mantinen en su lugar o están unidos a otros. Las fuerzas y pares ejercidos sobre un cuerpo por sus soportes se denominan reacciones, lo que expresa el hecho de que los soportes "reaccionan" a las otras fuerzas y pares, o cargas, que actúan sobre el cuerpo. Por ejemplo, un puente se sostiene gracias a las reacciones ejercidas por sus soportes, y las cargas son las fuerzas ejercidas por el peso del mismo puente, el tránsito que lo cruza, y el viento.
Algunos tipos muy comunes de sportes se representan con modelos estilizados llamados convenciones de soporte.
Soporte de pasador. Tenemos un soporte de pasador; un soporte al cual está unido un cuerpo (ej., una viga) con un pasador liso que pasa por el soporte y el cuerpo. La parte (b) es una vista lateral.
Para entender que reacciones pueden generar un soporte de pasador, imaginemonos sosteniendo una barra unida a un soporte soporte de pasador (fig. c). Si tratamos de mover la barra sin hacerla girar (es decir, trasladar la barra), el soporte ejerce una fuerzareactiva que lo impide. El soporte no puede generar un par respecto al eje del pasador para impedir el giro. Asi un soporte no puede generar un par respecto al eje del pasador pero si puede ejercer una fuerza sobre un cuerpo en cualquier dirección, lo que comúnmente se expre representando la fuerza en terminos de sus somponentes (d). La flecha indica las direcciones de las reacciones si Ax y Ay son positivas.
 |
| (a) Soporte de pasador. (b) Vista lateral que muestra el pasador atravesando la viga. (c)Sujetando una barra soportada. (d) El soporte de pasador es capaz de generar dos componentes de furza. |
Soporte de rodillo. Es un soporte de pasador montado sobre rueda. Como el soporte de pasador, el de rodillo no puede generar un par respecto al eje del pasador. Como se puede mover con libertad en la dirección paralela a la superficie sobre la que rueda, no puede generar una fuerza paralela a la superficie sobre la que rueda, no puede generar una fuerza paralela a la superficia sino una fuerza normal (perpendicular) a ella (b). Las figuras (c-e) son otras convenciones usadas comúnmente como equivalente al soporte de rodillo.
 |
| (a) Soporte de rodillos. (b) La reacción consiste en una fuerza normal a la superficie. (c-e) Soporte equivalentes al soporte de rodillos. |
Soporte de empotramiento. O tambien soporte fijo, presenta el objeto soportado literalmente empotrado en la pared como sre muestra en la figura de abajo. El termino Ma es el pargenerado por el soporte y la flecha curva indica su dirección. Los postes de barda y los del alumbrado público tiene soportes de empotramiento.
 |
| (a) Un empotramiento. (b) Sujetando una barra empotrada. (c) Racciones que un empotramiento es capaz de gener |
Ahora veremos algunos ejemplos.
1. La viga de la figura a tienes soportes y de rodillo, y está sometida a una fuerza de 2kN. ¿Qué valor tiene las reacciones en los soportes?
 |
| a |
SOLUCIÓN
Dibujo del diagrama de cuerpo libre. Aislamos la viga y mostramos las cargas y reacciones que pueden generar los soportes de pasador y de rodillo (fig. b). Hay tres reacciones desconosidas: dos componentes de fuerza, Ax y Ay, en el soporte de pasador y una fuerza B en el soporte de rodillo.
 |
| (b) Dibujo del diagrama de cuerpo libre de la viga. |
Aplicación de las ecuaciones de equilibrio. Sumando los momentos respecto al punto A, las escueciones de equillibrioson:
Resolviendo estas ecuaciones, las reacciones son Ax = 0.69 kN, Ay = 0.80 kN y B = 1.39 kN. La carga las reacciones se muestran el la figura de abajo. Es un buena costumbre mostrar las respuestas de esta manera y verificar que se cumplan las ecuaciones.
 |
| La crga y las reacciones. |
2. El cuerpo esta empotrado y sometido a dos fuerzas y un par. ¿Qué valor tiene las reacciones en el empotramiento?
SOLUCIÓN
Dibujat diagrama de cuerpo libre. Aislamos el cuerpo de su soporte y mostramos las reacciones en el empotramiento. Hay tres reacciones desconocidas: dos componente de fuerza Ax y Ay y un par Ma(recuerda que podemos escoger arbitrariamente las direcciones de esas flechas). Descomponemos tambien la fuerza de 100 lb en sus componentes.
Aplicar ecuaciones de equilibrio. Sumando los momentos respecto al puento A. las ecuaciones de equilibrio son:
Al resolver esas ecuaciones obtenemos las reacciones Ax = -86.6 lb, Ay = 150.0 lb, y Ma = 73.2 lb-pie
UNIDAD 2: ESFUERZO
Se conciderá en primer lugar que el área seccionada
está subdividida en áreas pequeñas, tal com el área ΔA mostrada en la figura 1-10a. Al reducir ΔA a un tamaño cada vez más pequeño, debe adoptarse dos supociones
respecto a las propiedades de la materia. Se considerá que el material es
cotinuo, es decir, que consiste en una distribueción uniforme o continuo de
material que no contiene huecos. Además, el material debe ser cohesivo, lo que
significa que todas sus partes están conectadas sí, sin fracturas, grientas o
separaciones. En la figura 1-10ª se muestra una fuerza típica finita pero muy
pequeña ΔF, la cual actúa sobre sú
area asociada ΔA. Esta fuerza, como
todas las demás. Tendrá uan dirección única, pero para el análisis que se
presenta a continuación se remplazará por sus tres componetes, ΔFx, ΔFy y ΔFz,
que se toman tangente, tangente y normal al área, respectivamente. Cuando ΔA y sus componetes hacen lo mismo; sin
embargo, el cociente de la fuerza y el área tenderán en general a un límite
finito. Este cociente se llama esfuerzo y
se describe la intencidad de la fuerza
interna sobre un plano específico (área) que pasa a través de un punto.
Esfuerzo normal. La intencidad de la fuerza que actúa en
forma normal a ΔA se define como el esfuerza normal, σ (sigma). Como ΔFz es normal al área, entonces:
ESFUERZOS NORMALES AXIALES
Definición 1: Esfuerzos normales, som aquellos debidos a fuerzas perpendiculares a la sección transversal.
Definición 2: Esfuerzo axiales, son aquellos debidos a fuerzas que actúan a lo largo del eje del elemento.
Los esfurzos normales axiales por lo general ocurren en elementos como cable, barra o columnas sometidos a fuerzas axiales (que actúan a lo largo de su propio eje), las cuales pueden ser de tensión o de comprención. Además de tener resistencia, los materiales deben tener rigidez, es decir capacidad de oponerse a las deformaciones (d) puesto que una estructura demasiado deformable puede llagar a ver comprometida su funcionalidad y obviamente su estética. En el caso de fuerzas axiales (de tensión o compresión), se producirán en el elemento alargamientos o a cortamientos, respectivamente, como se muestra en la figura 10.
Esfuerzo cortante. La intencidad de la fuerza que actúa tengente a ΔA se llama esfuerzo cortante, τ (tau). A continuación se presentan las componentes del esfuerzo cortante.
Acontinuación un video de apoyo de como calcular los esfuerzos normales:
ESFUERZOS NORMALES AXIALES
Definición 1: Esfuerzos normales, som aquellos debidos a fuerzas perpendiculares a la sección transversal.
Definición 2: Esfuerzo axiales, son aquellos debidos a fuerzas que actúan a lo largo del eje del elemento.
Los esfurzos normales axiales por lo general ocurren en elementos como cable, barra o columnas sometidos a fuerzas axiales (que actúan a lo largo de su propio eje), las cuales pueden ser de tensión o de comprención. Además de tener resistencia, los materiales deben tener rigidez, es decir capacidad de oponerse a las deformaciones (d) puesto que una estructura demasiado deformable puede llagar a ver comprometida su funcionalidad y obviamente su estética. En el caso de fuerzas axiales (de tensión o compresión), se producirán en el elemento alargamientos o a cortamientos, respectivamente, como se muestra en la figura 10.
 |
| Figura 10 |
Una forma de comparar la deformación entre dos elementos, es
expresarla como una deformación porcentual, o en otras palabras, calcular la
deformación que sufrirá una longitud unitaria del material, la cual se denomina
deformación unitaria e. La deformación unitaria se calculará como:
e = d /Lo
donde:
e:
deformación unitaria,
d:
deformación total.
Lo: longitud inicial del elemento deformado.
Acontinuación unos videos de apoyo:
Tracción
Comprención de probeta
Esfuerzo cortante. La intencidad de la fuerza que actúa tengente a ΔA se llama esfuerzo cortante, τ (tau). A continuación se presentan las componentes del esfuerzo cortante.
Observe que en esta notación
el subíndice z indica
la orientación del área ΔA, figura
1-11, y que x y y se usan para especificar los ejes a lo largo de los cuales actúan
cada esfuerzo cortante.
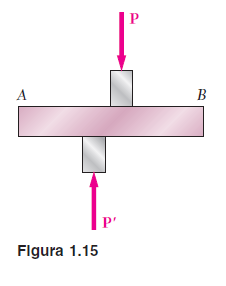
Otra explicacion del esfuerzo cortante las fuerzas internas y sus correspondientes esfuerzos estudiados en las secciones 1.2 y 1.3, eran normales a la sección considerada. Un tipo muy diferente de esfuerzo se obtiene cuando se aplican fuerzas transversales P y a un elemento AB (figura 1.15). Al efectuar un corte en C entre los puntos de aplicación de las dos fuerzas (figura 1.16a), obtenemos el diagrama de la porción AC que se muestra en la figura 1.16b. Se concluye que deben existir fuerzas internas en el plano de la sección, y que su resultante es igual a P. Estas fuerzas internas elementales se conocen como fuerzas cortantes, y la magnitud P de su resultante es el cortante en la sección. Al dividir el cortante P entre el área A de la sección transversal, se obtiene el esfuerzo cortante promedio en la sección. Representando el esfuerzo cortante con la letra griega t (tau), se escribe.
Debe enfatizarse que el valor obtenido es un valor promedio para el esfuerzo cortante sobre toda la sección. Al contrario de lo dicho con anterioridad para los esfuerzos normales, en este caso no puede suponerse que la distribución de los esfuerzos cortantes a través de una sección sea uniforme. Como se verá en el capítulo 6, el valor real t del esfuerzo cortante varía de cero en la superficie del elemento hasta un valor máximo tmáx que puede ser mucho mayor que el valor promedio, tprom.
Los esfuerzos cortantes se encuentran comúnmente en pernos, pasadores y remaches utilizados para conectar diversos elementos estructurales y componentes de máquinas (figura 1.17). Considere dos placas A y B conectadas por un perno CD (figura 1.18). Si a las placas se les somete a fuerzas de tensión de magnitud F, se desarrollarán esfuerzos en la sección del perno que corresponde al plano EE´. Al dibujar los diagramas del perno y de la
porción localizada por encima del plano EE´ (figura 1.19), se concluye que el cortante P en la sección es igual a F. Se obtiene el esfuerzo cortante promedio en la sección, de acuerdo con la fórmula (1.8), dividiendo el cortante P = F entre el área A de la sección transversal:

Acontinuacion un video de apoyo.
Propuestas de algunos problemas con solucion:
Problema 1.1
Problema 1.1
Estado general de esfuerzo. Si el cuerpo está seccionadoadicionalmente por planos paralelos al plano
x-z, figura 1-10b,
y al plano y-z, figura 1-10c,
entonces es posible “separar” un elemento cúbico de volumen de material en el
que se representa el estado de esfuerzo que
actúa alrededor del punto elegido en el cuerpo. De tal manera, este estado de
esfuerzo se caracteriza mediante tres compponentes que actúan sobre cada cara
del elemento, figura 1-12
Esfuerzo normal promedio en una barra cargada axialmente.
En esta secciónse determinará la distribucion del esfuerzo promedio que actúa sobre el área de la sección transversal de una barra cargada axialmente, como la que se muestra en la figuara a. Esta barra es prismatica porque todas las secciones transversales son iguales en toda su longitud. Cuando la carga P se aplica a la barra a través del centroide del área de su sección transversal, la barra se deformará de manera uniforme en toda la región central de su longitud, como se muestra b, siempre y cuando el material de la barra sea homogéneo e isotrópico.
Un material homogéneo tiene las mismas propiedades físicas de mecánicas en todo su volumen, y un material isotrópico tiene estas mismas propiedades en todas las direcciones.
Diatrivución del esfuerza normal promedio. Si se pasa una sección a través de la barra y se separa en dos partes, entonces el equilibrio requiere que que fuerza normal resultante en la secció sea P, figura c. Dada la deformación uniforme del material, es necesario que la sección transversal esté sometida a una distribucion del esfuerzo normal constante, figura d.
En esta secciónse determinará la distribucion del esfuerzo promedio que actúa sobre el área de la sección transversal de una barra cargada axialmente, como la que se muestra en la figuara a. Esta barra es prismatica porque todas las secciones transversales son iguales en toda su longitud. Cuando la carga P se aplica a la barra a través del centroide del área de su sección transversal, la barra se deformará de manera uniforme en toda la región central de su longitud, como se muestra b, siempre y cuando el material de la barra sea homogéneo e isotrópico.
Un material homogéneo tiene las mismas propiedades físicas de mecánicas en todo su volumen, y un material isotrópico tiene estas mismas propiedades en todas las direcciones.
DEFROMACIÓN SIMPLE
Objetivos del tema: Determinar las deformaciones inducidad en sistemas sometidos a cargas axiales.
DEFORMACIÓN SIMPLE
Deformación (δ) se refiere a los cambios en las dimensiones de un miembro estructural cuando este se encuentra sometido a cargas externas.
Estas deformaciones serán analizadas en elementos estructurales cargados axialmente, por los que entre las cargas estudiadas estarán las de tensión o compresión.
Un ejemplo de ellos:
- Los miembros de una armadura.
- Las bielas de los motores de los automóviles.
- Los rayos de las ruedas de bicicletas.
DEFORMACIÓN UNITARIA
Todo miembro sometido a cargas externas se deforma debido a la acción de esas fuerzas.
La Deformación Unitaria (ε), se puede definir como la relación existente entre la deformación total y la longitud inicial del elemento, la cual permitirá determinar la deformación del elemento sometido a esfuerzos de tensión o compresión axial.
Entonces, la fórmula de la deformación unitaria es:
TIPOS DE MATERIALES
 |
ε: Deformación Unitaria
δ: Deformación Total
L: Longitud inicial.
|
TIPOS DE MATERIALES
Se divide en dos tipos en FRACTILES y DUCTILES.
- Resistencia última, mayor que la ocurrida en el ensayo de tensión.
- No presenten punto de cedencia en ningún caso.
- El esfuerzo de rotura incide con el esfuerzo.
- Formación de conos de desprendimientos y destrucción de materiales debido a la llegada al límite de rotura.
- Su deformación es muy pequeña en comparación con los materiales dúctiles.
- Se fractura con mayor facilidad en comparación con un material dúctil.
a)Resistencia mecánica: la resistencia mecánica de un material es su capacidad de resistir fuerzas o esfuerzos. Los tres esfuerzos básicos son:
- Esfuerzo de Tensión: es aquel que tiende a estirar el miembro y romper el material. Donde las fuerzas que actúan sobre el mismo tienen la misma dirección, magnitud y sentidos opuestos hacia fuera del material. Como se muestra en la siguiente figura. Y viene dado por la siguiente formula:
- Esfuerzo de compresión: es aquel que tiende aplastar el material del miembro de carga y acortar al miembro en sí. Donde las fuerzas que actúan sobre el mismo tienen la misma dirección, magnitud y sentidos opuestos hacia dentro del material. Como se muestra en la siguiente figura. Y viene dado por la siguiente formula:
- Esfuerzo cortante: este tipo de esfuerzo busca cortar el elemento, esta fuerza actúa de forma tangencial al área de corte. Como se muestra en la siguiente figura. Y viene dado por la siguiente formula:
a) Rigidez: La rigidez de un material es la propiedad que le permite resistir deformación.
b)Elasticidad: Es la propiedad de un material que le permite regresar a su tamaño y formas originales, al suprimir la carga a la que estaba sometido. Esta propiedad varía mucho en los diferentes materiales que existen. Para ciertos materiales existe un esfuerzo unitario más allá del cual, el material no recupera sus dimensiones originales al suprimir la carga. A este esfuerzo unitario se le conoce como Límite Elástico.
Plasticidad: Esto todo lo contrario a la elasticidad. Un material completamente plástico es aquel que no regresa a sus dimensiones originales al suprimir la carga que ocasionó la deformación.
c)Ductilidad: Es la propiedad de un material que le permite experimentar deformaciones plásticas al ser sometido a una fuerza de tensión.
d)Deformación: son los cambios en la forma o dimensiones originales del cuerpo o elemento, cuando se le somete a la acción de una fuerza. Todo material cambia de tamaño y de forma al ser sometido a carga.
a) Límite de proporcionalidad: Se observa que va desde el origen O hasta el punto llamado límite de proporcionalidad, es un segmento de recta rectilíneo, de donde se deduce la tan conocida relación de proporcionalidad entre la tensión y la deformación enunciada en el año 1678 por Robert Hooke. Cabe resaltar que, más allá la deformación deja de ser proporcional a la tensión.
b) Limite de elasticidad o limite elástico: Es la tensión más allá del cual el material no recupera totalmente su forma original al ser descargado, sino que queda con una deformación residual llamada deformación permanente.
c) Punto de fluencia: es aquel donde en el aparece un considerable alargamiento o fluencia del material sin el correspondiente aumento de carga que, incluso, puede disminuir mientras dura la fluencia. Sin embargo, el fenómeno de la fluencia es característico del acero al carbono, mientras que hay otros tipos de aceros, aleaciones y otros metales y materiales diversos, en los que no manifiesta
.
d) Esfuerzo máximo o esfuerzo de Rotura: Es la máxima ordenada en la curva esfuerzo-deformación.
e) Esfuerzo de Rotura: En el acero al carbono es algo menor que la tensión de rotura, debido a que la tensión este punto de rotura se mide dividiendo la carga por área inicial de la sección de la barra, lo que es más cómodo, es incorrecto.
El error es debido al fenómeno denominado estricción. Próximo a tener lugar la rotura, el material se alarga muy rápidamente y al mismo tiempo se estrecha, en una parte muy localizada de la probeta, de forma que la carga, en el instante de rotura, se distribuye realmente sobre una sección mucho más pequeña.
Estado
inicial sin carga
Fenómeno
de Estricción
Falla
de la Probeta
LEY
DE HOOKE
La ley Hooke expresa que la deformación que experimenta un elemento sometido a carga externa es proporcional a esta.
En el año 1678 por Robert Hooke enuncia la ley de que el esfuerzo es proporcional a la deformación. Pero fue Thomas Young, en el año 1807, quien introdujo la expresión matemática con una constante de proporcionalidad que se llama Módulo de Young.En donde:
σ: es el esfuerzo.
ε: es la deformación unitaria.
E: módulo de elasticidad
ELEMENTO ESTÁTICAMENTE INDETERMINADOS
A continuación se presentan unos principios generales para enfrentar estos tipos de problemas:
2.Si hay más incógnitas que ecuaciones independientes de equilibrio, obtener nuevas ecuaciones mediante relaciones geométricas entre las deformaciones elásticas producidas por las cargas y por las fuerzas desconocidas: Realizar el diagrama de deformación.
ESFUERZO Y DEFORMACIÓN POR ORIGEN TÉRMICO
Algunos ejemplos de ellos son: las piezas de los motores, hornos, máquinas herramientas (fresadoras, tornos, cortadoras), equipos de moldeo y extrusión de plástico.
Coeficiente de expansión térmica (α): Es la propiedad de un material que indica la cantidad de cambio unitario dimensional con un cambio unitario de temperatura.
Las unidades en que se exprese el coeficiente de expansión térmica son:
E.U.G
SI
Expansión Térmica: Son las variaciones de dimensión en un material producto de los cambios de temperatura en el mismo. Y la ecuación es la siguiente:
ST = Expansión Térmica
a = Coeficiente de Expansión Térmica
L = Longitud inicial del miembro
ΔT = Cambio de temperatura
Unidad 3: EL ANÁLISIS DE DEFORMACIÓN
Concepto de deformación: La deformación es el cambio en ele tamaño o forma de un cuerpo debido a esfurzos inernos producidos por uno o más fuerzas aplicadas sobre el mismo o la ocurrencia de dilatación termica.
A continuació veran un video donde se presentan algunos ejemplos de ejercisios resueltos.
Deformación multiaxial.
DEFORMACIÓN UNITARIA CORTANTE
Carga multiaxial: Los elementos delgados sometidos a cargas axiales, es decir, a fuerzas dirigidas a lo largo de un solo eje. Escogiendo este eje como el eje X, y llamando P a la fuerza interna en una posición dada, los esfuerzos correspondientes resultaron ser σx=P/A, σy=0 y σz=0.
Se considerarán ahora elementos estructurales sometidos a fuerzas que actúan en las direcciones de los tres ejes coordenados produciendo los esfuerzos σx,σy y σz, todos diferentes de cero. Esta condición se denomina carga multiaxial. Sea un elemento de material en forma de cubo. Puede suponerse unitaria la arista del cubo. Bajo la carga multiaxial el elemento se convierte en un paralelepípedo rectangular de lados 1 + x, 1 + y y1 + z, en donde x, y, z, son las deformaciones normales en las direcciones de los ejes coordenados. Debe observarse que, como resultado de las deformaciones de otros elementos del material, el elemento estudiado puede también experimentar una traslación, pero aquí solo concierne la deformación real del elemento y no cualquier posible desplazamiento de cuerpo rígido. Para expresar los componentes de la deformación x, y, z en términos de los esfuerzos x, y, z se consideran separadamente el efecto de cada componente del esfuerzo y se combinan los resultados obtenidos.La aproximación que se utiliza en este punto se basa en el principio de la superposición. El efecto de una combinación de cargas en una estructura se puede obtener determinando separadamente los efectos de las diferentes cargas y combinando los resultados obtenidos siempre que se cumplan las siguientes condiciones: Cada efecto está linealmente relacionado con la carga que lo produce.
LEY DE HOOKE
Donde es la fuerza recuperadora que ejerce el resorte debido a la deformación y es la constante de elasticidad del resorte. La constante de elasticidad , es una característica del mismo, depende sólo de la forma del resorte y del material con que se ha construido. Debe ponerse el signo menos dado que el sentido de , como se ve en la ilustración, será siempre el opuesto al de la deformación .
Si una vez alcanzado el equilibrio, es decir cuando , tiramos de , produciendo en el resorte un alargamiento suplementario , con relación a la posición de equilibrio, y dejamos el sistema en libertad, observaremos que el resorte comienza a oscilar alrededor de la posición de equilibrio
La deformación de un cuerpo por lo general implica cambios en el tamaño y en la forma de éste. Los cambios de tamaño están asociados naturalmente con los alargamientos del cuerpo. Los cambios en la forma resultan no sólo de alargamientos sino también de cambios locales en los ángulos entre líneas del cuerpo que, inicialmente, son perpendiculares.
MÓDULO DE ELASTICIDAD
Las curvas de las figuras a y b son ejemplos del comportamiento elástico, cuando las cargas cesan, el material recupera su forma original. Una tira de caucho es aparentemente elástica; parece retornar a su longitud original al retirar una carga de tensión que actúe sobre ella. La figura es típica de un comportamiento inelástico, es decir, que queda una deformación permanente al cesar la carga. Un material dado se puede comportar en forma elástica un cierto intervalo de valores de esfuerzos y deformaciones unitarias y en forma inelástica en un intervalo mayor.
MÓDULO DE RIGIDEZ
Para un material elástico lineal e isótropo, el módulo de elasticidad transversal es una constante con el mismo valor para todas las direcciones del espacio. En materiales anisótropos se pueden definir varios módulos de elasticidad transversal, y en los materiales elásticos no lineales dicho módulo no es una constante sino que es una función dependiente del grado de deformación.
DISTRIBUCIÓN DEL ESFUERZO Y DE LA DEFORMACIÓN BAJO CARGA AXIAL
Se ha supuesto hasta ahora que en un elemento cargado axialmente los esfuerzos normales están uniformemente distribuidos en cualquier sección perpendicular al eje del elemento. Para determinar los esfuerzos reales en una sección dada del elemento es necesario solucionar un problema estáticamente indeterminado.
Los problemas estáticamente,indeterminados que incluyen la determinación de fuerzas pueden resolverse teniendo en cuenta las deformaciones causadas por estas fuerzas. Es razonable concluir entonces que para calcular los esfuerzos en un elemento es necesario analizar las deformaciones producidas por los esfuerzos.
TÉCNICA DE MEDICIÓN DE DEFORMACIÓN
DEFORMACIÓN.
Todo miembro de carga se deforma por la influencia de la carga aplicada. El eje cuadrado del pedestal apoyo de la figura 3.1, se acorta cuando sobre el se coloca equipo pesado. La deformación total de un miembro de carga puede, desde luego, ser medido. Más adelante se demostrará como puede calcularse la deformación La figura 3.11 nos muestra una fuerza de tensión axial de 10 000 Ib, aplicada a una barra de aluminio con un diámetro de 0.75 plg. antes de aplicar la carga, la longitud de la barra era de 10 plg.. Luego de aplicar la carga, la longitud es de 10.023 plg.. Por consiguiente, la deformación total es de 0.023 plg. la cual se calcula por la formula.
 |
| Alargamiento de una barra sometida a esfuerzo de tensión. |
La deformación que también se conoce como deformación unitaria, se obtiene dividiendo la deformación total entre la longitud original de la barra. La deformación se denota con la letra griega minúscula épsilon (e):
Coeficiente de Poisson.
Si se remite a la figura 3.12, se podrá obtener una comprensión más completa de la deformación de un miembro sujeto a esfuerzos normales. El elemento que se muestra está tomado de la barra de la figura 3.11. La fuerza de tensión en la barra la alarga en la dirección de la fuerza aplicada, como a de esperarse. Pero, al mismo tiempo, el ancho de la barra se acorta. De este modo, en el elemento de esfuerzo ocurre un alargamiento y contracción simultáneas. Puede determinarse la deformación axial a partir del alargamiento, y de la contracción, puede determinarse la deformación lateral.
El coeficiente de la deformación lateral en el elemento a la deformación axial se conoce como coeficiente de Poisson, y es una propiedad del material del que está hecho el miembro de carga.
En el presente texto, se utiliza la letra griega minúscula ni (v) para denotar el coeficiente de Poisson. Nótese que algunas referencias utilizan mi (jí). Los materiales metálicos más comúnmente usados, tienen un coeficiente de Poisson con valor entre 0.25 y 0.35. Para el concreto, varía ampliamente según el grado y el esfuerzo aplicados, pero generalmente cae entre 0.1 y 0.25. Los elastómeros, y el
caucho, tienen un coeficiente de Poisson que llega a ser hasta de 0.50. En la tabla 3-1 se muestra valores aproximados del coeficiente de Poisson.
Deformación por cortante.
Las demostraciones anteriores de deformación, describieron la deformación normal, porque esta es causada por el esfuerzo de compresión o tensión normal, desarrollado en un miembro de carga. Bajo la influencia del esfuerzo cortante, se produce la deformación por cortante.
Deformación por cortante.
Las demostraciones anteriores de deformación, describieron la deformación normal, porque esta es causada por el esfuerzo de compresión o tensión normal, desarrollado en un miembro de carga. Bajo la influencia del esfuerzo cortante, se produce la deformación por cortante.
La figura 3.13 muestra un elemento sujeto a esfuerzo cortante. La acción cortante en las caras paralelas del elemento tienden a deformarlo angularmente, como se muestra de forma exagerada. El ángulo y (gamma), medido en radianes, es la deformación por cortante. En los problemas prácticos se encuentran sólo valores sumamente pequeños de deformación por cortante y, por consiguiente, las dimensiones del elemento sólo se cambian levemente.
Módulo de elasticidad.
Puede obtenerse una medida de la rigidez del material, calculando el coeficiente del esfuerzo normal en un elemento, y la deformación correspondiente en el mismo dentro del límite proporcional del material. Esta relación se conoce como módulo de elasticidad, y se denota por E.
Es decir:
Un material con un valor de E elevado se deformará menos con un esfuerzo dado, que con un valor reducido de E. Un término más completo para E sería el módulo de elasticidad a tensión o compresión, porque se define en función del esfuerzo normal. Sin embargo, el termino "módulo de elasticidad", sin ningún modificador, generalmente se considera como el módulo de tensión.
Módulo de elasticidad a cortante.
El coeficiente del esfuerzo cortante y la deformación por cortante se conoce como módulo de elasticidad a cortante, módulo de rigidez, y se denota por G.
Es decir:
G es una propiedad del material, y se relaciona con el módulo de tensión y el coeficiente de Poisson por:
Fuerzas en un cuerpo.
Un cuerpo sólido puede estar cargado por fuerzas de cuerpo (gravedad, fuerza centrifuga etc.), por fuerzas de superficie, o por ambas. Las fuerzas resultantes internas serán referidas como esfuerzos. Para nuestro propósito, el esfuerzo será definido como una fuerza que actúa sobre una área unitaria. Ver figura 3.14.
Donde:
a = Esfuerzo normal (Ibs./plg2)
P = Carga (Ibs.)
A = Area de la sección transversal normal al eje de carga (plg2)
Ejemplos de esfuerzos son: tensión, compresión, flexión, corte y torsión.
Un cuerpo sólido sujeto a un esfuerzo manifestará deformación. La magnitud de la deformación depende principalmente de las propiedades elásticas del material. Cualquier cambio dimensional será referido como deformación unitaria.
Deformación unitaria es referida como un cambio en longitud sobre la longitud
unitaria debido a las fuerzas aplicadas.
Donde:
e = Deformación unitaria axial, (plg/plg)
DL = Cambio de longitud, (plg)
L= Longitud unitaria (plg)
La relación entre esfuerzo y deformación unitaria está ilustrada en una curva típica de esfuerzo - deformación unitaria. Inicialmente, la relación entre las fuerzas aplicadas y la deformación dimensional aparece como una relación lineal. Esta región elástica termina en el límite proporcional donde termina la linealidad. Eventualmente hay incrementos de elongación sin incremento apreciable en la carga aplicada, (referido como el punto de fluencia, sí el esfuerzo se incrementa otra vez con una deformación unitaria adicional). El pico de la curva indica el máximo esfuerzo y es llamada "resistencia ultima". Debajo de este punto la curva desciende hasta el punto de fractura. Mientras que el esfuerzo real o verdadero continúa incrementándose por arriba de la"resistencia ultima", la curva indica los esfuerzos basados en el área de la sección transversal original. Ver figura 3.15.
DEFORMACIONES DE ELEMENTOS SOMETIDAS A CARGA AXIAL
Considere una varilla homogénea BC de longitud L y sección transversal uniforme de área A sujeta a una carga axial centrada P (figura 2.22). Si el esfuerzo axial resultante σ = P/A no excede el límite de proporcionalidad del material, se aplica la ley de Hooke y se escribe.
de donde sigue que
 |
| 2.7 |
La ecuación (2.7) se usará sólo si la varilla es homogénea (E constante), tiene una sección transversal uniforme con área A y está cargada en sus extremos. Si la varilla está cargada en otros puntos, o si consta de varias porciones con distintas secciones transversales y, posiblemente, distintos materiales,
debe dividirse en partes que satisfagan de manera individual las condiciones requeridas para la aplicación de la fórmula (2.7). Si, Pi, Li, Ai y Ei representan, respectivamente, la fuerza interna, longitud, área de sección transversal y módulo de elasticidad que corresponden a la parte i, la deformación de la varilla entera será.
La deformación total d de la varilla se obtiene al integrar esta expresión por la longitud L de la varilla:
 |
| 2.9 |
La fórmula (2.9) deberá emplearse en lugar de (2.7), no sólo cuando el área de la sección transversal A es una función de x, sino también cuando la fuerza interna P dependa de x, como es el caso de una varilla suspendida y sometida a la acción de su propio peso.
Ejemplo: 1
Determine la deformación de la varilla de acero mostrada en la figura 2.23a bajo las cargas dadas (E = 29 x
10-6 psi ).
Se divide la varilla en tres partes (la figura 2.23b) y se tiene
Para encontrar las
fuerzas internas P1, P2 y P3, se deben hacer cortes a través de cada
una de las partes, dibujando cada vez un diagrama de cuerpo libre
de la porción de la varilla localizada a la derecha de la sección
(figura 2.23c). Expresando que cada uno de los cuerpos libres está en equilibrio, se obtiene sucesivamente.
Llevando los valores obtenidos a la ecuación (2.8), se tiene que
Deformación y esfuerzo térmica
OBJETIVOS DE ESTE CAPITULO
El estudio de la resistencia de los
materiales comprende la determinacion tanto de esfuerzos en elementos
estructurales de carga como de la deflexion o deformacion de los mismos. En general,
se requiere el analisis tanto del esfuerzo como de la deformacion
unitaria, tal como se definieron en el capitulo 1. El material expuesto
en los capitulos 1, 2 y 3 permite calcular la magnitud de los esfuerzos que se
generan en elementos estructurales sometidos a fuerzas axiales directas, sean
de tension o compresion. Este capitulo amplia el conocimiento de tales
elementos estructurales al incluir la deformacion. En este capitulo se
presentan dos clases de deformacion, la deformacion elastica, provocada
por las cargas externas y la deformacion termica, provocada por los
cambios de temperatura. Cuando un material se calienta tiende a expandirse y
luego que se enfria tiende a contraerse. Si se permite que las deformaciones
termicas ocurran sin restriccion, no se produciran esfuerzos. Pero si se impide
que el miembro estructural se mueva, se desarrollaran esfuerzos. Estos
esfuerzos se llaman esfuerzos termicos. Los principios de la deformacion
elastica tambien se pueden usar para resolver algunos problemas mas o menos
complejos en los que elementos estructurales hechos de mas de un material se
someten a cargas. Dichos elementos estructurales a menudo son estaticamente
indeterminados, es decir, no se pueden determinar las fuerzas ni los
esfuerzos internos con ecuaciones de estatica simples. Se demostrara el uso
combinado de la estatica, el analisis del esfuerzo y el analisis de la deformacion
elastica para resolver problemas como los antes mencionados.
Despues
de terminar el estudio de este capitulo, el lector sera capaz de:
1. Calcular la cantidad de deformación elástica de un miembro estructural sometido a una carga de tensión o compresión axial.
2. Diseñar elementos estructurales sometidos a cargas axiales para limitar su deformación aun valor específico.
3. Definir el coeficiente de expansión térmica y seleccionar el valor propio a usarse en el cálculo de la deformación térmica.
4. Calcular la cantidad de deformación térmica de un elemento sujeto a cambios de temperatura cuando la deformación no es restringida.
DEFORMACION ELASTICA EN ELEMENTOS
SOMETIDOS A TENSION Y COMPRESION
Deformacion se refiere a cualquier
cambio en las dimensiones de un miembro estructural de carga. El poder calcular
la magnitud de la deformacion es importante en el diseno de mecanismos de
precision, maquinas-herramienta, estructuras de edificios y estructuras de
maquinas.
En la figura 3-2 se muestra una
troqueladora con tensores de acero de seccion transversal circular conectados a
ella, donde la deformacion es importante. Los tensores experimentan tension
cuando la troqueladora se encuentra en operacion. Como los tensores contribuyen
a la rigidez de la troqueladora, la deformacion que sufren a consecuencia de
una carga es algo que el disenador ha de ser capaz de determinar.
Para deducir la relacion con la que
se pueda calcular la deformacion en elementos sometidos a tension o compresion
axial, se tienen que revisar algunos de los conceptos del capitulo 1. La deformacion
unitaria se define como la razon de la deformacion total a la longitud
original de un elemento. Con el simbolo e para la deformacion unitaria, 5
para la deformacion total y L para la longitud, la formula para la
deformacion unitaria se convierte en:
 |
| 1) |
La rigidez de un material es una función de su módulo de elasticidad E, que se define como:
 |
| 2) |
Al resolverse para la deformación unitaria se obtiene:
 |
| 3) |
Ahora se pueden igualar las ecuaciones 1 y 3
 |
| 4) |
Al resolverse para la deformación se obtiene:
 |
| 5) |
 |
| 6) |
La ecuacion 6) se usa para calcular
la deformacion total de cualquier elemento de carga, siempre que satisfagan las
condiciones que se definen en relacion con el esfuerzo directo de tension y
compresion. Es decir, el elemento ha de ser recto y de seccion transversal constante;
el material debe ser homogeneo, la carga axial directa y el esfuerzo menorque
el limite proporcional del material. Recuerde que el valor del limite
proporcional se aproxima a la resistencia a la cedencia, sy.
Ejemplo: 1
La aceptabilidad de esta cantidad de deformación axial se tendría que de terminar mediante un análisis del sistema de toda la troqueladora.
Los tensores de la troqueladora son de aleacion de acero aisi5160oqt1000. El diametro de cada tensor
es de 2.00 plg y su longitud inicial de 6 8 .5 plg. Se aplica una fuerza de tension
axial de 40000 ib a cada tensor durante el funcionamiento de la troqueladora .
Calcule la deformacion de los tensores.
·
Objetivo:
Calcular la
deformacion de las varillas.
· Datos:
Los tensores son
de acero, AISI5160OQT1000; diametro = D
= 200pig Longitud = L = 68 .5 plg. Fuerza
axial = F = 40000 Ib.
·
Analisis:
Se usara la
ecuacio n 6) y se
verificara el esfuerzo que actua en los
· tensores
para asegurarse de que este abajo del limite p roporcional.
·
ResuItados: Esfuerzo de
tension axial: a =
F/A.
Deformacion axial: Use la ecuación 6). Todos los datos
se conocene xcepto el modulo de elasticidad E.
E = 30x106 psi. Entonces:
La aceptabilidad de esta cantidad de deformación axial se tendría que de terminar mediante un análisis del sistema de toda la troqueladora.
Unidad 4: TORSION
Para esta sección es valida la hipótesis de Coulomb, la cual se verifica experimentalmente tanto en el
caso de secciones circulares macizas como huecas. La hipótesis referida establece que las secciones normales al eje de la pieza permanecen planas y paralelas a sí misma luego de la deformación por torsión. Además, luego de la deformación, las secciones mantienen su forma. Como consecuencia de lo enunciado resulta que las secciones tienen rotaciones relativas, de modo que las rectas trazadas sobre ellas continúan siendo rectas y los ángulos mantienen su medida. Por otro lado, las generatrices rectilíneas de la superficie lateral del cilindro se transforman en hélices.
A partir de las consideraciones anteriores, que están relacionadas con la compatibilidad de las deformaciones, deseamos saber qué tipo de tensiones genera la torsión simple y cual es su distribución. Supongamos en primera instancia que aparecen tensiones normales σ. Su distribución no podría ser uniforme ya que de ser así existiría una resultante normal a la sección. Al distribuirse entonces en forma variable, según la Ley de Hooke, las deformaciones especificas ε variaran también punto a punto, y la sección no continuaría siendo normal al eje, no siendo válida la hipótesis de Coulomb, que indica que la sección se mantiene plana.
En virtud de lo anterior sólo resta considerar que en el problema de torsión aparecen únicamente tensiones tangenciales. A su vez, para que las tensiones constituyan un sistema estáticamente equivalente al momento torsor Mt debe ocurrir que:
Resulta evidente que si tomamos un elemento diferencial en coincidencia con el borde de la sección, la tensión tangencial τ deberá ser tangente a la circunferencia, ya que de no ser así existirá una componente de τ radial, la que, por Cauchy, originaría una tensión tangencial aplicada sobre una generatriz del cilindro. Esto que ocurre en el borde puede admitirse que también acontece en el interior, con lo que las tensiones tangenciales beberían ser normales al radio. Además, para que puedan cumplirse las ecuaciones 5.1 y 5.2 debe ocurrir que las tensiones tangenciales sean antimétricas a lo largo de los diámetros de la sección.
De lo visto podemos obtener algunas conclusiones:
- sólo existen tensiones tangenciales
- su distribución a lo largo de un diámetro es antimétrica
- su dirección es normal al radio
Torsion se refiere al torcimiento de una barra recta al ser cargada por momentos (o pares de torsion) que tienden a producirrotacion con respecto al eje longitudinal de la barra. Por ejemplo, cuando usted gira un destornillador (figura 3.1a), su mano aplica un par de torsion T al mango (figura 3.1b) y tuerce el vastago del destornillador. Otros ejemplos de barras en torsion son los ejes de impulsion en automoviles, ejes de transmision, ejes de helices, barras de direccion y brocas de taladros.
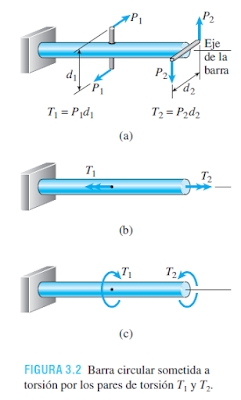
Un caso idealizado de carga torsional se representa en la figura 3.2a, donde se muestra una barra recta soportada en un extremo y cargada por dos pares de fuerzas iguales y opuestas. El primer par consiste en las fuerzas P1 que actuan cerca del punto medio de la barra y el segundo para consiste de las fuerzas P2 que actuan en el extremo. Cada par de fuerzas forma un par de torsión que tiende a torcer la barra con respecto a su eje longitudinal. Como sabemos de la estatica, el momento de un par de torsión es igual al producto de una de las fuerzas y la distancia perpendicular entre las linea de accion de las fuerzas; por tanto, el primer par de torsion tiene un momento T1 = P1d1 y el segundo tiene un momento T2 = P2d2.
Las unidades en el sistema inglés para el momento son la libra-pie (lb-ft) y la libra-pulgada (lb-in). La unidad en el SI para el momento es el newton metro (N∙m).
El momento de un par de torsión se puede representar por un vector en forma de una flecha con cabeza doble (figura 3.2b). La flecha es perpendicular al plano que contiene el par de torsión y, por tanto, en este caso las dos flechas son paralelas al eje de la barra. La dirección (o sentido) del momento se indica mediante la regla de la mano derecha para vectores momento: empleando su mano derecha, permita que sus dedos se curven en el sentido del momento y entonces su dedo pulgar apuntará en la dirección del vector.
Una representación alternativa de un momento es una flecha curva que actúa en el sentido de la rotación (figura 3.2c). La flecha curva y las representaciones vectoriales son de uso común y en este libro emplearemos las dos. La elección depende de la conveniencia y la preferencia personal.
Los momentos que producen el torcimiento de una barra, como los marcados T1 y T2 en la figura 3.2, se llaman pares de torsión o momentos de torsión. Los elementos cilíndricos que se someten a pares de torsión y transmiten potencia mediante rotación se llaman ejes; por ejemplo, el eje impulsor
de un automóvil o el eje de la hélice de un barco. La mayor parte de los ejes tienen secciones transversales circulares sean sólidas o tubulares.
Deformaciones unitarias por cortante en la superficie exterior
Ahora considere un elemento de la barra entre dos secciones transversales separadas una distancia dx (consulte la figura 3.4a). Este elemento se muestra agrandado en la figura 3.4b. En su superficie exterior identificamos un elemento pequeño abcd, con lados ab y cd que al inicio son paralelos al eje
longitudinal. Durante el torcimiento de la barra, las secciones transversales derechas giran con respecto a las secciones transversales izquierdas un ángulo pequeño de torsión df, de manera que los puntos b y c se mueven a b' y c’, respectivamente. Las longitudes de los lados del elemento, que ahora es el elemento ab'c'd, no cambian durante esta rotación pequeña. Sin embargo, los ángulos en las esquinas del elemento (figura 3.4b) ya no son iguales a 90°.
Por tanto, el elemento está en un estado de cortante puro, lo cual significa que el elemento está sometido a deformaciones por cortante
pero no a deformaciones normales (consulte la figura 1.28 de la seccion 1.6).
La magnitud de la deformacion por cortante en la superficie exterior de la
barra, denotada ymax, es igual al
decremento en el angulo en el punto a, es decir,
el decremento en el angulo bad.
De la figura 3.4b observamos que el decremento en este angulo es
La fórmula de la torsión
El paso siguiente en nuestro análisis es determinar la relación entre los esfuerzos cortantes y el par de torsión T. Una vez determinada esta relación, podremos calcular los esfuerzos y las deformaciones unitarias en una barra debidas a cualquier conjunto de pares de torsión aplicados.
El momento resultante (igual al par de torsión T) es la suma a lo largo de
toda el área de la sección transversal de todos los momentos elementales:
 |
| 1) |
en donde
 |
| 2) |
es el momento polar de inercia de la sección transversal circular. Para un círculo con radio r y diámetro d, el momento polar de inercia es
 |
| 3) |
Es posible obtener una expresión para el esfuerzo cortante máximo reacomodando
la ecuación 1), como sigue:
Esta ecuación, conocida como la fórmula de la torsión, muestra que el esfuerzo cortante máximo es proporcional al par de torsión aplicado T e inversamente proporcional al momento de inercia polar IP.
Ángulo de torsión
Ahora podemos relacionar el ángulo de torsión de una barra de material linealmente elástico con el par de torsión aplicado T. Con la fórmula de la torsión obtenemos
en
donde u tiene
unidades de radianes por unidad de longitud. Esta ecuacion muestra
que la razon de torsion u es directamente proporcional al par de
torsion T e
inversamente proporcional al producto GIP, conocido como rigidez torsional de la barra. Para
una barra en torsión
pura, el angulo de torsion f total, igual a
la razon de torsion
multiplicada por la longitud de la barra (es decir, f = uL), es
en donde el angulo se mide en radianes.
Ejemplos:
FLEXION EN VIGA
—Las vigas son elementos estructurales muy usados en las construcciones para soportar cargas o darle estabilidad a las mismas; para diseñarlas es necesario conocer las fuerzas perpendiculares a los ejes x y que se ejercen a lo largo de su longitud.
Ejemplos:
Una
barra solida de acero con seccion transversal circular (figura 3.11) tiene un
diametro d = 1.5 in, longitud
L = 54 in y
modulo de elasticidad en cortante G = 11.5
× 106 psi. La barra esta sometida a
pares de torsion T que actuan en
sus extremos. (a) Si los pares de torsion tienen una magnitud T
= 250 lb-ft, .cual es el esfuerzo cortante
maximo en la barra? .Cual es el angulo de torsion entre los extremos? (b) Si el esfuerzo cortante permisible es
6000 psi y el angulo de torsion permisible es 2.5°, .cual es el par de torsion
maximo permisible?
Solución
(a) Esfuerzo cortante máximo y ángulo de torsión. Dado que la barra tiene una sección transversal circular sólida, podemos determinar el esfuerzo cortante con, como sigue:
De una manera similar, el ángulo de torsión con el momento polar de inercia.
Por tanto, el análisis de la barra ante la acción del par de torsión dado está completo.
(b) Par de torsión máximo. El par de torsión máximo se determina mediante el esfuerzo cortante permisible o bien por el ángulo de torsión permisible. Iniciando con el esfuerzo cortante, y el cálculo es el siguiente:
Cualquier par de torsión mayor que este valor resultará en un esfuerzo cortante que sobrepasará el esfuerzo permisible de 6000 psi.
Con la siguiente ecuación ahora podemos calcular el par de torsión con base en el ángulo de torsión:
Cualquier par de torsión mayor que T2 resultará en un ángulo de torsión mayor que el permisible.
El par de torsión máximo es el menor de T1 y T2:
En este ejemplo el esfuerzo cortante permisible proporciona la condición limitante.
UNIDAD 5 ESFUERZOS POR FLEXIÓN EN VIGA
—Las vigas son elementos estructurales muy usados en las construcciones para soportar cargas o darle estabilidad a las mismas; para diseñarlas es necesario conocer las fuerzas perpendiculares a los ejes x y que se ejercen a lo largo de su longitud.
Cuando es importante estudiar las deflexiones:
La figura muestra una viga con perpendiculares al eje y ubicada en el plano de simetría de la sección:- En estructuras metálicas.
- Sistemas de tuberías.
- Ejes/ arboles para maquinas.
- — Distancia entre apoyos.
- — Materiales de la viga.
- — La carga aplicada.
- — Propiedades geométricas de las vigas.
- — Tipos de vinculación (apoyos).
En elemento de la viga mostrado en la figura, se deforma de tal manera que cualquier punto en una sección transversal entre apoyos se desplaza prácticamente paralelo a las cargas.
—Estos desplazamientos se denomina las deflexiones o flechas del momento.
—Al estar las cargas ubicadas en el Eje Principal de Inercia, hace que las secciones transversales se desplacen verticalmente.
Como las deformaciones verticales , en la sección transversal son sensiblemente menores que las deformaciones longitudinales , todos los puntos de la sección transversal tienen prácticamente el mismo desplazamiento vertical.
Un caso típico son las vigas, las que están diseñadas para trabajar, principalmente, por flexión. Igualmente, el concepto de flexión se extiende a elementos estructurales superficiales como placas o laminas.
El rasgo más destacado es que un objeto sometido a flexión presenta una superficie de puntos llamada fibra neutral tal que la distancia a lo largo de cualquier curva contenida en ella no varía con respecto al valor antes de la deformación. El esfuerzo que provoca la flexión se denomina momento flector.
Aqui un ejemplo:
Deflexion de vigas
Flexión en vigas y arcos
ANGULO DE FLEXION
Se denomina ángulo de flexion al angulo que forma la linea de una poligonal con la prolongación de la linea o segmento anterior. El angulo se mide desde la prolomgacíon de la linez anterio hasta la linea. Se llama deflexión positiva o derechacuando el angulo se mide en sentido horario y negativo o izquierda cuando el angulo se mide en sentido contra horaio.
La figura 18 presenta la defliexión positiva o deracha en una poligonal abierta y la 19, presenta la deflexión o izquierda en el poligono cerrada.
Para las conversiones entre azimut y rumbo se debe proceder de acuerdo al cuadrante, tal como se muestra a continuación.
Deflexion de vigas
Flexión en vigas y arcos
Las vigas o arcos son elementos estructurales pensados para trabajar predominantemente en flexión.
Geométricamente son prismas mecanicos cuya rigidez depende, entre otras cosas, del momento
de inercia de la sección transversal de las vigas. Existen dos hipótesis cinemáticas comunes para
de inercia de la sección transversal de las vigas. Existen dos hipótesis cinemáticas comunes para
representar la flexión de vigas y arcos:
· La hipótesis de Navier-Euler-Bernouilli. En ella las secciones transversales al eje baricentrico s
consideran en primera aproximación indeformables y se mantienen perpendiculares al mismo (que se
curva) tras la deformación.
consideran en primera aproximación indeformables y se mantienen perpendiculares al mismo (que se
curva) tras la deformación.
· La hipótesis de Timoshenko. En esta hipótesis se admite que las secciones transversales
perpendiculares al eje baricéntrico pasen a formar un ángulo con ese eje baricéntrico por efecto del
esfuerzo cortante.
perpendiculares al eje baricéntrico pasen a formar un ángulo con ese eje baricéntrico por efecto del
esfuerzo cortante.
La teoría de Euler-Bernoull para el cálculo de vigas es la que se deriva de la hipótesis cinemática de
Euler-Bernouilli, y puede emplearse para calcular tensiones y desplazamientos sobre una viga o arco
de longitud de eje grande comparada con el canto máximo o altura de la sección transversal.}
ANGULO DE FLEXION
Se denomina ángulo de flexion al angulo que forma la linea de una poligonal con la prolongación de la linea o segmento anterior. El angulo se mide desde la prolomgacíon de la linez anterio hasta la linea. Se llama deflexión positiva o derechacuando el angulo se mide en sentido horario y negativo o izquierda cuando el angulo se mide en sentido contra horaio.
La figura 18 presenta la defliexión positiva o deracha en una poligonal abierta y la 19, presenta la deflexión o izquierda en el poligono cerrada.
Para las conversiones entre azimut y rumbo se debe proceder de acuerdo al cuadrante, tal como se muestra a continuación.
Calculo de flexión de viga (ejemplo 1)
Calculo de flexión (ejemplo 2)
Calculo de flexión (ejemplo 3)
Calculo de flexión (Ejemplo 4)
Cargas combinadas (ejemplo 1)
UNIDAD 6: ESFUERZOS COMBINADOS
CIRCULO DE MOHR PARA ESFUERZOS
El círculo de mohr es un metodo gráfico para determinar el
estado tensional en los distintos puntos de un cuerpo. Entre las tenciones que
existen en un cuerpo sometido a un cierto estado de cargas y con unas ciertas
restriciones, importan en geeral las tenciones principales, que son las
tanciones que existe sobre ciertos planos del cuerpo, donde las tenciones de
corte nulas. Estas tensiones son de importancia para el estudio de la
resistencia mecánica de una pieza.
A continuacion uno ejersicios resueltos de Esfuerzos por flexion en vigas
CILCULO DE MOHR
El Círculo de Mohr es una técnica usada en ingeniería y geofísica para representar gráficamente un tensor simétrico (de 2x2 o de 3x3) y calcular con ella momentos de inercia, deformaciones y tensiones, adaptando los mismos a las características de una circunferencia (radio, centro, etc). También es posible el cálculo del esfuerzo cortante máximo absoluto y la deformación máxima absoluta.
Este método fue desarrollado hacia 1882 por el ingeniero civil alemán Christian Otto Mohr (1835-1918).
El Círculo de Mohr es una técnica usada en ingeniería y geofísica para representar gráficamente un tensor simétrico (de 2x2 o de 3x3) y calcular con ella momentos de inercia, deformaciones y tensiones, adaptando los mismos a las características de una circunferencia (radio, centro, etc). También es posible el cálculo del esfuerzo cortante máximo absoluto y la deformación máxima absoluta.
Este método fue desarrollado hacia 1882 por el ingeniero civil alemán Christian Otto Mohr (1835-1918).
 |
| Círculos de Mohr para representar un estado de tensión tridimensional en un punto. |
Introducción
A partir de esta definición, la noción de estructura tiene innumerables aplicaciones. Puede tratarse de la distribución y el orden de las partes principales de un edificio o de una casa, así como también de la armadura o base que sirve de sustento a la construcción. Por ejemplo: “A simple vista parece un edificio muy moderno, pero habría que analizar su estructura”, “Me encanta la estructura de esta casa, con el baño ubicado junto a la habitación principal”, “Una falla en la estructura causó el derrumbe de una torre en Kuala Lumpur”.
Columnas
Introducción.
Una columna (misma palabra en latín, derivada de columen, "sostén", "soporte") es un elemento arquitectónico vertical y de forma alargada que normalmente tiene funciones estructurales, aunque también pueden erigirse con fines decorativos. De ordinario, su sección es circular, pues cuando es cuadrangular suele denominarse pilar, o pilastra si está adosada a un muro.
La columna clásica está formada por tres elementos basa, fuste y capitel.
En arquitectura clásica, la basa es la parte inferior de la columna, que tiene como fin servir de punto de apoyo al fuste, ampliando aquel, y está compuesto generalmente por molduras.
- El fuste es la parte de la columna que se encuentra entre el capitel y la basa.
- Corresponde al cuerpo principal o básico de las columnas utilizadas en muchos de los edificios desde la época egipcia hasta el neoclásico del siglo XIX. Su diseño puede ser desde el simplemente liso o con decoracion.
El capitel (del latín caput, capitis = cabeza) es un elemento arquitectónico que se dispone en el extremo superior de la columna, pilar o pilastra para transmitir a estas piezas estructurales verticales las cargas que recibe del entablamento horizontal o del arco que se apoya en él.
Otros ejemplos de columnas con diferentes estilos arquitectónicos:
1.-hindú
2.-persa
3.-egipcio
4.-cretense
5.-románico
6.-gótico
7.-renacentista
8.-barroco
1.-hindú
2.-persa
3.-egipcio
4.-cretense
5.-románico
6.-gótico
7.-renacentista
8.-barroco












































































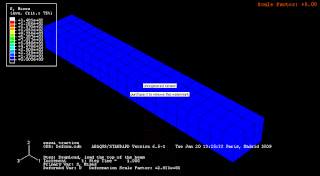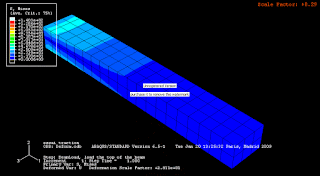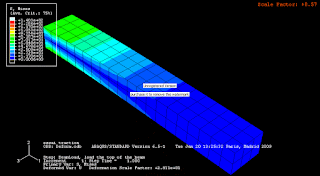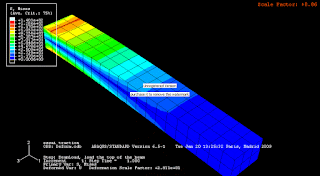










Muy bien Luipta, fuiste muy responsable en entregar tu trabajo. Felicidades, sigue así.
ResponderEliminarBuenas muy bueno todooo, me gustaria saber como hacen para sacar la deformacion total?
ResponderEliminarQue lindo la materia
ResponderEliminarWynn Casino And Hotel Las Vegas - JM Hub
ResponderEliminarCasino. Wynn Hotel. Casino. Wynn 안동 출장샵 Hotel. Casino. 광주광역 출장안마 Las Vegas, NV 여수 출장안마 89109. 서귀포 출장마사지 Telephone: 서산 출장안마 (702) 770-9946. Website. www.wynnlasvegas.com.